第三章 荣方问陈子日高

昔者榮方問於陳子，曰：『今者竊聞夫子之道。知日之高大，光之所照，一日所行，遠近之數，人所望見，四極之窮，列星之宿，天地之廣袤，夫子之道皆能知之。其信有之乎？』
陳子曰：『然。』
榮方曰：『方雖不省，願夫子幸而說之。今若方者可教此道邪？』
陳子曰：『然。此皆算術之所及。子之於算，足以知此矣。若誠累思之。』

白話翻譯
古代的榮方問陳子說：『我聽說先生您的科學知識和方法，能知太陽的遠近大小，還有日光普照所及的範圍，太陽一日運行的遠近度數，人眼睛所能望見的天地極限，以及天上的星宿，天地的廣袤，先生的道術_{科學知識和方法}都能知曉，真是如此嗎？
陳子說：『是的。』
榮方說『榮方雖然愚鈍，卻也希望有幸能夠瞭解這些科學原理和方法，您看象我這樣的人能夠授予我這些科學知識和方法嗎？』
陳子說：『可以的。這只需要基本的數學知識，我看您的數學基礎足以理解這些科學原理和方法了。您先自己去反復思考，或許就可以領悟。』

於是榮方歸而思之，數日不能得。
復見陳子曰：『方思之不能得，敢請問之。』
陳子曰：『思之未熟。此亦望遠起高之術，而子不能得，則子之於數，未能通類。是智有所不及，而神有所窮。夫道術，言約而用愽者，智類之明。問一類而以萬事達者，謂之知道。今子所學，算數之術，是用智矣，而尚有所難，是子之智類單。夫道術所以難通者，既學矣，患其不博。既博矣，患其不習。既習矣，患其不能知。故同術相學，同事相觀。此列士之愚智，賢不肖之所分。是故能類以合類，此賢者業精習智之質也。夫學同業而不能入神者，此不肖無智而業不能精習。是故算不能精習，吾豈以道隱子哉？固復熟思之。』

白話翻譯
於是榮方回去反復思索，數日不能得要領。
又去見陳子說：『榮方思索未能領悟，敢請夫子開導講授。』
陳子說：『思考得不夠成熟。其實基礎也就是望遠測高之術，而您不能領悟，而您對數學還不能觸類旁通，或者是智有所不及，還是想的太多太遠了。您所問的那些原理和方法，原則簡約而用途廣泛，特別要求觸類旁通的智慧。瞭解了一類而能通曉萬事，就是參悟了原理和方法。您所學過的數學基礎和方法，本來就需要智慧，而參悟起來尚有困難，說明您的智慧還太單純有限，須知原理和方法之所以難通，就在於學了卻不能廣博，廣博了卻不能熟練，熟練了卻不能參悟精義。因此能否在相似的方法中悟出共同原則，在同類事物中推得普遍規律，這是區別人的智慧和愚鈍，有才能的人和普通人的分水嶺。所以能夠類推演繹，是聖賢者能夠探尋到事物的規律的基本素質，同樣的事情，聖賢者能達到理想境界，普通人就不能如此。我豈會向您隱瞞科學原理和方法呢？您且回去再反復思索吧!』

榮方復歸，思之，數日不能得。
復見陳子曰：『方思之以精熟矣。智有所不及，而神有所窮，知不能得。願終請說之。』
陳子曰：『復坐，吾語汝。』於是榮方復坐而請。
陳子說之曰_{從形式上說，自此以下的所有論述皆為陳子所作。為便於據文義進行分段以清眉目，不再標點作直接引語形式}：『夏至南萬六千里，冬至南十三萬五千里，日中立竿測影。此一者天道之數。周髀_{周髀，為垂直立於地上的竿狀物，亦稱為表。其得名之故以及各種用途可見下文}長八尺，夏至之日晷_{晷，指八尺之表在日光下投於地面的影長。趙爽注：『晷，影也。』}一尺六寸。髀者，股也。正晷者，句也。正南千里，句一尺五寸。正北千里，句一尺七寸。日益表南，晷日益長_{在天地為平行平面的假設下，並取天高H=80000里、表高h=8尺這組參數時，『日影千里差一寸』的結論確實可以得到證明。『正南千里……』兩句，是指同一天(故日位置固定不動)在不同地點(自周地向南千里和向北千里)測日影的情形。『日益南，晷益長』則是指同在周地而不同季節(故日南北遠近不同)測日影的情形}。候句六尺_{若已掌握普適的畢氏定理，則日影(勾)為任何長度時皆可施行下文的計算；而此處非要『候勾六尺』不可，足見仍只掌握了勾三、股四、弦五的特例，故需湊成其倍數以便套用}，即取竹，空徑一寸，長八尺，捕影而視之，空正掩日，而日應空之孔。由此觀之，率八十寸而得徑一寸_{由相似三角形可知，太陽至觀測者距離與太陽直徑之比等於竹筒長度與竹筒孔徑之比}。故以句為首，以髀為股。從髀至日下六萬里，而髀無影。從此以上至日，則八萬里。若求邪_{邪，此處音、義俱同『斜』}至日者，以日下為句，日高為股。句、股各自乘，并而開方除之，得邪至日，從髀所旁_{旁，趙爽注：『旁，此古邪字。』據前一『邪』字的用法，完全可通。錢寶琮據顧觀光之說，謂『旁』及『邪』俱當作『袤』，似乎反而使問題複雜化了}至日所十萬里。以率率之，八十里得徑一里。十萬里得徑千二百五十里。故曰，日晷徑千二百五十里。』

白話翻譯
於是榮方回去又思索數日，仍是不能領悟。於是再去見陳子說道：『榮方確實盡力深思了，實在是智有所不及，思維受到限制，實在是無法自行參悟了，還是請先生開導講授吧!』
陳子說：『請坐，我來告訴您。』於是榮方坐下再次請教，陳子開始講授他的原理。
陳子告訴他說：『我們是在周地建立觀測站，周地在什麼地方呢？是在北半球冬至日正中午太陽到達的極限位置。從周地算起，夏至之日假定水準向南16000里，冬至之日假定水準向南135000里，日中_正中午時立竿測影，由於太陽在正上方，立竿的影子垂直於假定的水平面，與立竿重合。這就是太陽運行軌道的規律。那麼怎麼知道這個規律的呢？使用的是一種測量方法，稱為周髀，具體做法是精製一根8尺長的測杆，在周地觀測站垂直于水準地面直立，夏至之日的正中午，可以觀測到立竿在水準地面的影子長度是1.6尺，立竿就是一個直角三角形的直立邊，稱為股。立竿的影子的長度構成了直角三角形的另一條邊，為勾。假設我們在水平面把這根立竿向正南方向移動1000里，這時立竿水平面的影子應該是1尺5寸。假設我們在水平面把這根立竿向正北方向移動1000里，這時立竿在假定水平面的影子應該是1尺7寸。這就是說太陽越往南，我們在周地測得的立竿的影子越長。按照這個比例關係，也就是說我們立竿影子的1寸，相當於實際尺寸的1000里，1尺相當於10000里。這是一個測量的原理，這樣告訴您，您能理解嗎？實際操作不可能是這樣的，您想一想地球是一個球體，1000里的距離就不是一個水平面了，而是一個曲面了，因此實際求解這個比例關係是在地面上在短距離的範圍內，把地面假定成一個平面，採用下圖所示方法求得。

根據相似三角形原理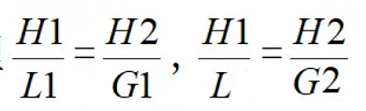

L2在地面作為基線邊可以精確丈量，G1、G2為晷影長度，H1=H-H2，L=L1+L2。兩式求解可以求出：

此式表明從測杆頂至太陽的距離H1與H2的比值等於兩個測點之間的距離與兩點測杆晷影之差的比值。這個公式證明太陽影像所處的高度就是距離地面80000里，這個資料就是根據太陽晷影長度在平面的變化規律測算出來的。同樣採用8尺測杆觀看太陽晷影長度正好是6尺的時候測點至太陽的斜距，太陽至測點平面的垂直距離，測點至太陽的垂線與平面交點的距離就構成了一個直角三角形，他們的尺寸關係就是斜距長100000里，高差為80000里，平面距離為60000里。這個就是太陽影像_焦點與地平面的關係。這是客觀存在。
有了上述的原理，那麼在周地就可以等候一個時間，那就是當太陽在地面影子長度剛好是6尺時，我們用一根空心的管子，這個管子的內經為1寸，長度為8尺，對著太陽從管子的一端觀看太陽，這時太陽和管子的內徑剛好重合。通過這樣的觀測，太陽與管子的直徑的比例關係是80:1。我們就可以計算出太陽的直徑。什麼原理呢？這跟我們選擇的這個時間有關係，我們選擇的這個時間，立竿8尺，影子長6尺，那麼立竿頂點至地面影子的斜長構成一個直角三角形，那麼這個直角三角形的斜長就是10尺(1丈，根據前面介紹的原理，立竿高8尺，說明太陽的高度距我們決定的水準地面為80000里，立竿的影子長6尺，說明太陽距測站的水準距離為60000里，我們就知道此時觀測點至太陽的距離為100000里，根據比例關係我們就可以求得太陽的直徑為100000除以80等於1250里_{這是太陽在大氣層內影像的直徑，與太陽的實際距離和直徑之比值成正比例關係，因此其方法計算太陽的視直徑是正確的數值}。當然這是為了便於您理解而選擇的時間，其實任何時間在觀測站我們都可以通過比例關係測出太陽的直徑，只是資料計算比較複雜，因此我們的觀測站往往就是利用這麼一些比較極限的時間點來觀測，因此對星球的規律容易找到。

日高圖：